Here's to you, Dr. Robinson
We'd like to know a little bit about you for our files (on pro vaccine misinformation)
Introduction
I recently offered to help Steve Kirsch and team in a public debate on whether the COVID vaccine saved more lives than it killed. This is an important endeavor: up to 47% of American US adults still don’t think there is a link between the COVID vaccine and a significant number of unexplained deaths. Meaningful improvements and reforms in US healthcare will not happen until more Americans do.
My task is to help rebut a graph presented by the pro COVID vaccine side that shows that, during the July-September 2021 Delta surge, states with lower vaccination rates had higher COVID deaths in adults over 65 years of age. The graph (shown below) was produced by KFF which dubs itself as the “the leading health policy organization in the U.S.”
COVID-19 deaths for adults 65 and older per 100,000 between July 1, 2021 and September 25, 2021, among the 65 and older population of each state

Based on this negative correlation, the KFF authors conclude the graph is evidence that vaccinated individuals are less likely to die from COVID. They also explain there are only 38 states because “States were excluded from this analysis where there was a discrepancy of more than 10% between the total number of COVID-19 deaths by age group and the total number of deaths overall within the state.” but don’t provide a rationale for this decision. More importantly, the plot is an example of “Robinson’s paradox”, a form of “ecological fallacy” (Robinson, 1950). An ecological correlation is a correlation between m pairs of percentages (and/or proportions as in the graph above). From Wikipedia on Robinson’s Paradox and Ecological Fallacy:
A 1950 paper by William S. Robinson computed the illiteracy rate and the proportion of the population born outside the US for each state and for the District of Columbia, as of the 1930 census.[7] He showed that these two figures were associated with a negative correlation of −0.53; in other words, the greater the proportion of immigrants in a state, the lower its average illiteracy (or, equivalently, the higher its average literacy). However, when individuals are considered, the [expected] correlation between illiteracy and nativity was +0.12 (immigrants were on average more illiterate than native citizens). Robinson showed that the negative correlation at the level of state populations was because immigrants tended to settle in states where the native population was more literate. He cautioned against deducing conclusions about individuals on the basis of population-level, or "ecological" data.
In other words, one should not draw conclusions about individual behavior (i.e. is an individual more likely to die from COVID if they are unvaccinated?) from an ecological correlation because of the risk of spurious correlations.
I suspected that the negative correlation in the KFF graph is also a spurious correlation. To explore this, I reproduced the KFF graph, but instead used adjusted mortality rates from a time period before vaccines were available. The below graph plots the same percent vaccination rates on the X-axis as the graph above, but the Y-axis has been replaced with age-adjusted mortality rates for the same states in 2020.
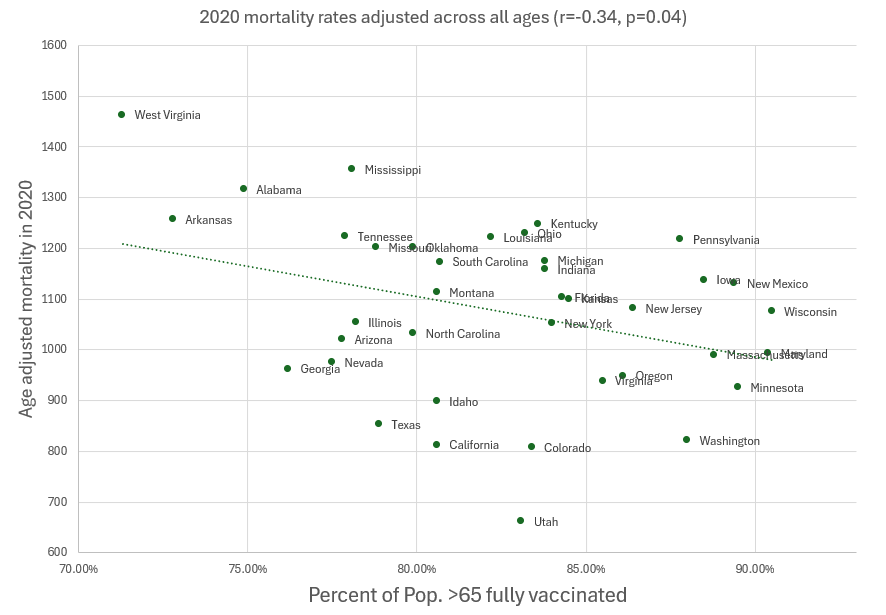
Clearly, the significant negative correlation (r=-0.34, p=0.04) cannot be attributed to vaccines because they were not introduced until 2021. Instead, the variation is attributed to state-to-state variation in mortality due to differences in chronic conditions such as lower respiratory disease, heart disease, cancer, obesity etc. which are also comorbidities that increase risk of death from COVID-19.
What is the relationship between COVID vaccines and COVID deaths?
To preclude Robinson’s paradox, we need to plot individual-level counts of vaccine doses vs. individual-level counts of COVID (or total) deaths in each state. We also need to adjust for each state’s population size. Without such an adjustment, vaccination doses in each state will be tightly correlated with COVID deaths by virtue of the fact that larger states will happen to have more vaccine doses and deaths than smaller ones. However, we can’t standardize by comparing percentages and proportions for the reasons stated above.
Instead, we can use multiple linear regression to test if vaccine doses in one month predict COVID (or non-COVID) deaths in a subsequent month and adjust for state-to-state variation in population and mortality by including prior year (2020) deaths as an additional term.
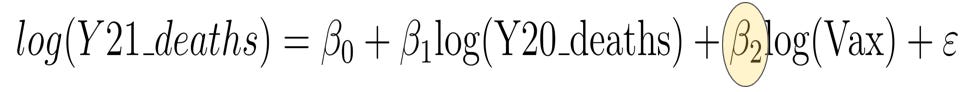
Using this approach, we see strong positive correlations between vaccine doses and COVID deaths as shown below:

What is the relationship between COVID vaccines and total deaths?
However, we are much more interested in all cause mortality, not just COVID deaths. Even if we assume that the vaccine reduces your likelihood of dying from COVID, but these odds are offset by increasing your likelihood of dying from myocarditis or stroke etc., is it still a good idea to take the vaccine?
The figure below plots the months with significant associations between prior month vaccine doses and current month total deaths in 2021 for each age group (right Y-axis).

We can observe that all significant beta slopes (p<0.05 FDR adjusted) were positive. We also can observe that the temporal pattern of significant slopes falls out of the analysis in a data driven way: the pattern fits the vaccine rollout by age group in that we only observe significant slopes for adults >65 yrs prior to April, and then in adults >18 yrs old after April (the vaccine was rolled out to adults >18 yrs old on April 16th, 2021). Note that the figure only plots results up to August, 2021 because that was the latest data that was available when I started analyzing the data for the preprint (September of 2021).
What is the relationship between COVID vaccines and COVID cases?
Using a spreadsheet that Steve provided, I used the same procedure as above but instead examined the relationship between vaccine doses and COVID cases for the entire year (2021) compared to 2020, before the COVID vaccines became available.
As expected, this results in a strong positive association supporting the idea that COVID vaccination increases your chances of contracting COVID. There is an overall weakening of the immune system within the 3-4 weeks post-injection, making COVID infection more likely during this period. I speculate that vaccine “protection’ observed in many vaccine effectiveness/efficacy (VE) studies may actually be a consequence of “natural” immunity following COVID infection in the first weeks following vaccination.
Because of the 5-6 week delay in immune “protection” post first vaccine dose, the majority of VE studies censor this period or categorize individuals within 5 weeks post-injection as “unvaccinated”. Neil et al. 2024 recently reanalyzed 38 VE studies to determine the effect of such “categorization bias”. They found that categorizing individuals within 5-weeks post-first dose injection as “vaccinated” instead of “unvaccinated” yielded zero or negative VE.
Conclusion
The ecological fallacy of Robinson’s paradox prevents us from deducing conclusions about individual behavior based on correlations between population-level (ecological) data, such as area-level rates or proportions. Be careful when interpreting such graphs.




Please get in touch about publishing this as a formal, reviewed esearch letter here http://publichealthpolicyjournal.com- JLWPhD
You should write this up and publish it, if possible. Quite interesting.